Atividades práticas Os conceitos matemáticos devem ser construídos na prática. Repetições mecânicas não garantem o aprendizado. Repetir a um aluno que 1 + 1 = 2, não significa que ele vai apreender os conceitos envolvidos nessa operação. Então, quanto mais atividades práticas e contextualizadas maiores as chances de sucesso para o aluno com discalculia.
As atividades propostas a seguir podem ser adaptadas e aprimoradas de acordo com os objetivos e potencialidades dos alunos. Os materiais são comuns ao contexto escolar, porém, caso sua escola não tenha poderá construir conforme as sugestões. Atenção: a mediação do professor e de outros colegas será essencial para que o aluno chegue ao raciocínio esperado. As atividades também poderão ser usadas com alunos que não possuem discalculia.
Material Dourado Com o material dourado é possível trabalhar atenção, classificação, seriação, conservação e raciocínio lógico
1° Sugestão Conhecendo o material
Roteiro: construa com o aluno um cartaz ilustrativo contendo um exemplar de cada peça colado com fita adesiva transparente. Não se esqueça de colocar os valores correspondentes a cada uma das peças. Cubinho - unidade, Barra - dezena, Placa - centena e Cubo - milhar. Deixe o cartaz exposto em sala de aula.
2° Sugestão Correspondência de quantidades
Roteiro: utilize materiais da própria sala de aula, quantidade de lápis de cor, livros de histórias e outros. A quantidade de alunos é uma boa sugestão. Peça que o aluno conte quantos meninos e meninas vieram e represente em uma folha essa quantidade. Suponha que a quantidade encontrada foram meninos 11 e meninas 12. Agora, com esse papel o aluno deverá representar a quantidade com o material dourado.
Observação: caso na representação o aluno tenha usado apenas cubinhos, auxilie o raciocínio de que ele pode trocar as representações da seguinte maneira: meninos - trocar os 11 cubinhos por uma barra de dezena e um cubinho de unidade; meninas - trocar 12 cubinhos por uma barra de dezena e dois cubinhos de unidade. A sugestão para construção do material dourado está disponível para download.

Descrição da imagem: material de madeira com representação de cubinhos, barras, placas e cubo.
Baixar
Quadro Valor de Lugar - QVL Auxilia na compreensão do sistema de numeração decimal
1° Sugestão Conhecendo o material
Roteiro: entregue ao aluno os números de 0 a 9 recortados e uma folha do QVL. Peça que o aluno represente no QVL os número que você falar. Comece por números que contenham apenas unidades e depois coloque números maiores.
Observação: comece pelo QVL de unidade e dezena, depois de acordo com os objetivos poderá utilizar o QVL de unidade, dezena, centena e unidade de milhar. Todos os materiais para as atividades propostas estão disponíveis para download.
2° Sugestão Jogo de quantidades com o QVL e o material dourado.
Roteiro: Entregue uma folha de QVL para cada aluno. Explique as regras: O jogo pode ter até cinco participantes. O número de rodadas pode ser combinado entre os jogadores. Em cada rodada deve ser lançado o dado, com o resultado o jogador pode pegar as pecinhas correspondentes do material dourado. Em seguida deve representar o valor a lápis no seu QVL. Ao final das rodadas ganha o jogador que tiver o maior valor.
Observação: com o avanço das rodadas os alunos serão expostos a variadas transformações de unidades em dezenas, dezenas em centenas e assim por diante. Acompanhar e orientar o aluno nesse processo será essencial.
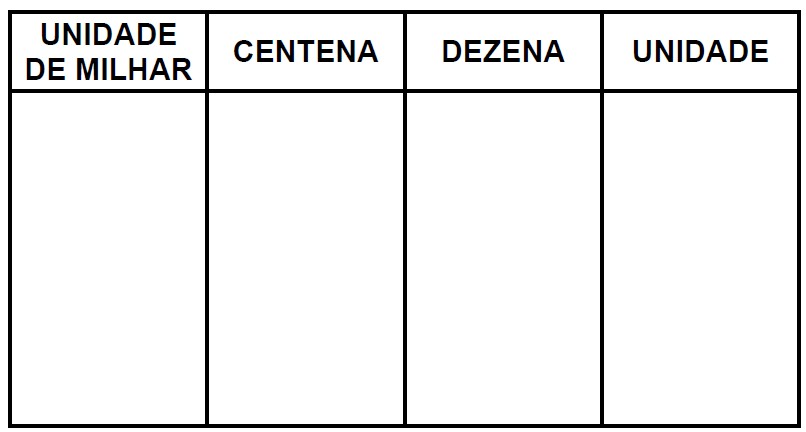
Descrição da imagem: folha dividida em quarto partes. As partes representam a casa da unidade, dezena, centena e unidade de milhar.
Quadro Valor de Lugar com números
1° Sugestão Representação de quantidades com material dourado e o QVL com números
Roteiro: represente uma quantidade com o material dourado e peça que o aluno aponte essa quantidade no QVL com números. Agora troque, represente um número no QVL e peça que o aluno aponte a quantidade no material dourado.
2° Sugestão Ditado de números
Roteiro: dite números que o aluno deverá representar no QVL com números.
Observação: as instruções e materiais para construção do QVL com números estão disponíveis para download.
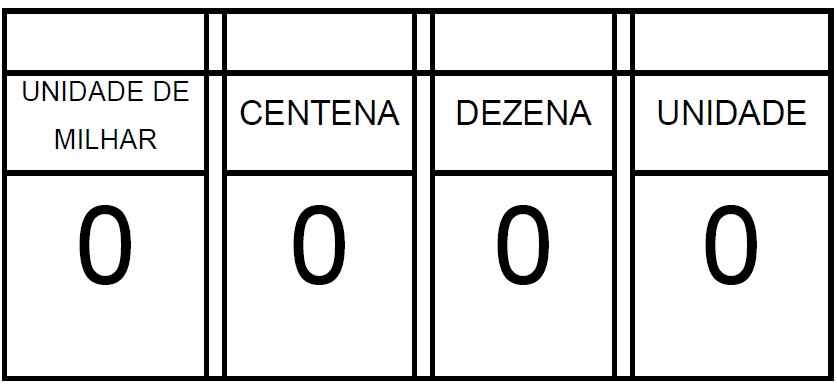
Descrição da imagem: folha dividida em quatro colunas, unidade, dezena, centena e milhar. Cada coluna com o número zero.
Baixar
Blocos Lógicos Trabalha a atenção, motricidade, análise, acuidade visual, sequência lógica e diferentes conceitos
1° Sugestão Explorando o material
Roteiro: peça que o aluno organize as peças em grupos pelo critério que ele preferir.
Observação: perceba a lógica usada no critério escolhido pelo aluno e sugira também agrupar por cor, forma e espessura.
2° Sugestão Trabalhando sequências
Roteiro: coloque uma sequência na mesa com os blocos lógicos, dê um tempo para que os alunos memorizem e esconda a sequência, depois peça que reproduzam.
Observação: explore bem as diferentes características do material e crie variadas sequências. Os alunos podem criar suas próprias sequências para que os amigos reproduzam.
3° Sugestão Ache a peça
Roteiro: Crie pistas que indiquem a posição de peças previamente escondidas em sala de aula. Cada aluno pegará uma pista e terá que achar a peça. Trabalhe noções espaciais como em cima, embaixo, ao lado de, perto de, longe de, entre outros. Exemplo de pista: estou entre o armário e a porta.
Observação: as pistas podem ficar mais elaboradas e indicar a posição, formato da peça, a espessura e cor, por exemplo: todos os meus lados têm tamanho igual, sou da cor de uma banana, da espessura como de um palito e estou embaixo de uma mesa. Assim, o aluno ou o grupo podem concluir juntos que se trata de um quadrado, amarelo, fino e que está embaixo da mesa. As instruções e materiais para construção dos Blocos Lógicos estão disponíveis para download.

Descrição da imagem: peça de madeira com formas geométricas em triângulos, quadrados, retângulos e círculos nas cores amarela, vermelho e azul.
Baixar
Ábaco aberto É possível explorar o valor posicional, a compreensão do sistema de numeração decimal e com maiores possibilidades as operações de adição e subtração
1° Sugestão Conhecendo o material
Roteiro: monte um cartaz ilustrativo dos valores de cada argola com os alunos e deixe exposto em sala de aula.
Observação: as instruções e materiais para construção do ábaco aberto estão disponíveis para download.
2° Sugestão Contando argolas
Roteiro: coloque todas as argolas que representam unidades em um saco ou em uma caixa tapada, peça que cada aluno retire cinco argolas, o aluno deverá somar o valor das argolas e chegar à conclusão de que tem cinco unidades. Após, coloque as argolas de unidades de volta na sacola e misture com as dezenas, repita todo o processo. Agora o aluno terá que somar argolas com valor de unidade e de dezena, além de representá-las no ábaco, se necessário auxilie nesse processo. Repita todo o processo com as argolas de centena, unidade de milhar e dezena de milhar conforme os objetivos.
3° Sugestão Representando quantidades no ábaco
Roteiro: separe os alunos em grupos de até cinco, coloque o ábaco e suas peças no centro da mesa, cada aluno jogará o dado e representará o valor correspondente no ábaco, com o avanço das rodadas os alunos irão se deparar com a problemática de mudança de valor.
Observação: o aluno deverá compreender que deve redistribuir os valores em suas novas posições. Contudo, se esse conceito não vier de imediato à condução do raciocínio por parte do professor ou de um par competente será de grande ajuda.
4° Sugestão Problemas de adição e subtração
Roteiro: use problemas matemáticos contextualizados. Por exemplo: João tem uma coleção de 18 carrinhos, represente o número 18 simultaneamente à apresentação do problema no ábaco, em seguida conclua, ele ganhou mais 11 carrinhos. Pergunte: como podemos descobrir com quantos ele ficou usando o ábaco? Com a colaboração chegarão à conclusão de que basta incluir os novos carrinhos no ábaco e contar com quantos ficou.
Observação: dificulte com problemas em que as unidades se transformam em centenas e assim sucessivamente. Com a subtração a lógica não será diferente. Tomemos como exemplo o problema: Carlos possui 49 peças de lego e emprestou 26 para seu primo. Com quantas peças de lego Carlos ainda ficou? Durante o problema repita o mesmo processo de colocar o número 49 no ábaco e peça ajuda para solucionar.
Observação: dificulte com problemas em que seja necessário o processo de “emprestar” da centena para a dezena e sucessivamente. Os alunos poderão ser ativos em manipular o ábaco nas resoluções e também em criar novos problemas a serem solucionados.

Descrição da imagem: base de madeira com cinco pinos que representam unidade, dezena, centena, unidade de milhar e dezena de milhar. Cada uma contendo dez argolas com cores específicas.